Το τέλος του μαρτυρίου

Δείτε όλα τα καλοκαιρινά προβλήματα, αλλά και τις προηγούμενες λύσεις. Παρακάτω και οι τελευταίες.

1. Αριθμητικό φιδάκι

Σε οκτάχρονα(!) στο Βιετνάμ δόθηκε ο παρακάτω πίνακας και τους ζητήθηκε να τον συμπληρώσουν με τους ακεραίους αριθμούς 1 έως 9 , χρησιμοποιώντας τον καθένα μόνον μια φορά, ώστε να προκύψει μετά τις πράξεις ο αριθμός 66. Ξεκινούμε από το τετράγωνο αριστερά, κατεβαίνουμε προς τα κάτω, μετά δεξιά, στην συνέχεια επάνω, πάλι δεξιά κλπ. Τοποθετώντας τους αριθμούς στα άδεια τετράγωνα και εκτελώντας τις πράξεις.

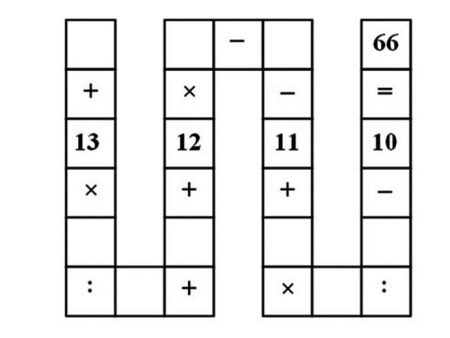
Θα φανταστούμε ότι στα κενά αρχίζοντας από επάνω αριστερά και ακολουθώντας το «σώμα» του φιδιού αντιστοιχούν τα γράμματα α, β, γ, δ, ε, ζ, η, θ, ι. Άρα μια πρώτη σχέση, με βάση τις πράξεις που είναι σημειωμένες θα είναι: α+(13β/γ) + δ + 12ε – ζ -11 + (ηθ/ι) = 66.

Μια πρώτη τακτοποίηση της παραπάνω σχέσης δίνει:

α +δ – ζ + (13β/γ) + 12ε + (ηθ/ι) = 66 +11 +10 = 87

Για τα κλάσματα θα ζητήσουμε να είναι τελικά ακέραιοι αριθμοί.

Επίσης το (13β/γ) δεν θα πρέπει να είναι μεγάλο όπως κα το (ηθ/ι) διότι έχουμε μόνον μια αφαίρεση στο πρώτο μέλος. Δοκιμάζουμε β=2 και γ=1 και προκύπτει ότι: α+δ-ζ +26 +12ε +(ηθ/ι) = 87 ή α+δ-ζ+12ε +(ηθ/ι) = 61 και να μην ξεχνάμε ότι μας μένουν οι αριθμού από το 3 έως το 9. Τους πρώτους αριθμούς 3, 5, 7 τους αντιστοιχούμε στα α,δ και ζ.

Άρα 3+5-7 + 12ε + (ηθ/ι) = 60. Μας έμειναν οι 4,6,8,9. Εδώ θέλει κάποιο ψάξιμο με δοκιμές που δίνουν τελικά ε=4, η=9, θ=8 και ι=6 .

4. Κινέζικο μαρτύριο

Στην Κίνα δόθηκε σε εντεκάχρονα το παρακάτω με σημειωμένα επάνω σε κάποια από τα σχήματα τα εμβαδά τους. Ζητείται το εμβαδόν του κόκκινου τριγώνου.

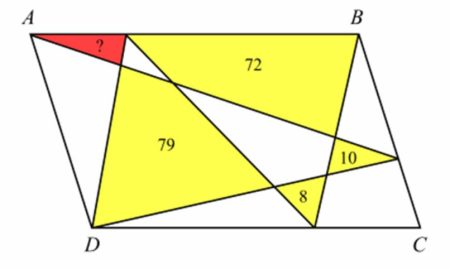
Ένα πρώτο βήμα είναι να αντιστοιχηθούν με γράμματα όλες οι υπόλοιπες επιφάνειες στο σχήμα. Το δεύτερο βήμα είναι η παρατήρηση πως ένα τρίγωνο που η μια πλευρά του είναι και πλευρά του παραλληλογράμμου και η απέναντι κορυφή του βρίσκεται στην απέναντι πλευρά του παραλληλογράμμου έχει εμβαδόν ίσο με το μισό του εμβαδού όλου του παραλληλογράμμου. Αυτό προκύπτει εύκολα από τον τύπο για το εμβαδόν ενός τριγώνου(βάση επί το ύψος δια 2).

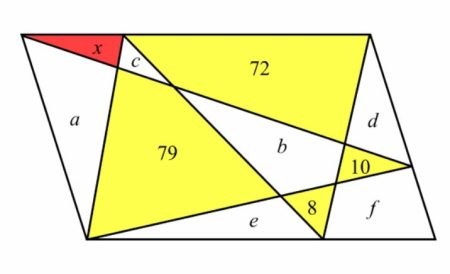
Στην εικόνα παρατηρούμε δυο τέτοια τρίγωνα: Το ένα συντίθεται από τις επιφάνειες a, 79, b, 10 με συνολική επιφάνεια (α + 79 +b +10) και στην άλλη περίπτωση έχουμε δυο τρίγωνα, με επιφάνειες (x+α) και (72+b+8) με βάσεις σε μια από τις δυο μεγαλύτερες πλευρές και κορυφές στην απέναντι πλευρά. Το άθροισμα των επιφανειών και των δυο αυτών τριγώνων( (x+α), (72+b+8)) είναι επίσης ίσο με το μισό του εμβαδού του παραλληλογράμμου(διότι οι βάσεις τους συνολικά έχουν μήκος όσο η μια πλευρά και ύψος το ύψος του παραλληλογράμμου). Εξισώνουμε επομένως τις επιφάνειες:

(72+b+8) + (x+α) = (α + 79 +b +10) από όπου προκύπτει ότι x = 89 – 80 = 9

8. Το κολύμπι της ανδροπαρέας

Σε ένα διάστημα 100 ημερών μέσα στο καλοκαίρι ο καθένας από 6 φίλους πηγαίνει για κολύμπι ακριβώς 75 ημέρες. Είναι ν οι ημέρες όπου είναι στην θάλασσα τουλάχιστον 5 από τα μέλη της παρέας αυτής. Ποια μπορεί να είναι η μεγαλύτερη και ποια η μικρότερη τιμή του ν;

Απάντηση

Επειδή ο καθένας από τους 6 φίλους κολυμπάει οπωσδήποτε 75 ημέρες πολλαπλασιάζουμε 6 επί 75 = 450 και βρίσκουμε τον αριθμό των «ημερών»(δηλαδή αν βάζαμε ένα αστεράκι για κάθε φορά που κάποιος έρχεται στην πισίνα σε ένα απουσιολόγιο τα αστεράκια αυτά συνολικά ή αλλιώς οι ημέρες παρουσίας τους θα ήταν 450) Μένει τώρα να δούμε πώς κάποια από αυτά τα 450 μπορούν να κατανεμηθούν μέσα σε ένα σύνολο ημερών με τον ελάχιστο και με τον μέγιστο τρόπο αρκεί σε αυτές τις ημέρες να είχαν κολυμπήσει πάντοτε 5 ή 6 άτομα από την παρέα.

Οι ημέρες που κάποιος από τους 6 δεν κολύμπησε ήταν 100 – 75 = 25 , άρα και για τους 6 ήταν 25×6=150. Για να έχουμε τον μέγιστο αριθμό των ημερών που κολύμπησαν μόνον 4 θα πρέπει να σκεφθούμε ότι σε αυτές τις ημέρες οι άλλοι 2 δεν παρουσιάστηκαν ταυτόχρονα. Πόσες μπορεί να ήταν αυτές; (150/2) = 75 ημέρες όπου κολυμπούσαν το πολύ 4 ταυτόχρονα. Άρα τις υπόλοιπες 100 – 75 =25 στην πισίνα βρέθηκαν 5 ή 6 ταυτόχρονα.

Για τον μέγιστο αριθμό των ημερών που μπορούσαμε να έχουμε τουλάχιστον 5 (αλλά και 6) στην πισίνα την ίδια ημέρα αρκεί να διαιρέσουμε τις 450 ημέρες παρουσίας δια 5 οπότε βρίσκουμε 90. Άρα 25<= ν <=90, δηλαδή οι ελάχιστες ημέρες ήταν 25 και το μάξιμουμ 90.

Προσοχή: Στο Διαδίκτυο εμφανίζονται και κάποιες άλλες απαντήσεις για το ίδιο πρόβλημα αλλά βασίζονται σε λάθος συλλογισμούς.

Για τους μαθητές που δούλεψαν και το καλοκαίρι…

Δηλαδή για όποιους τα είχαν λύσει ήδη όλα μέσα στο καλοκαίρι, έπρεπε να έχουμε κάτι και για εκείνους. Τρία προβλήματα σε επίπεδο γνώσεων το πολύ Γυμνασίου λοιπόν, εκ των οποίων τα δυο αρκετά ενδιαφέροντα:

1. Χωρίς μολύβι και χαρτί: Πόσες ακέραιες τιμές του x εκπληρούν τις ανισότητες: (1/2)<(3x/100)<(4/5);

2. Το άθροισμα των 100 πρώτων ακεραίων αριθμών (2+3+5+7+11+13+…) που είναι και «πρώτοι»(δηλαδή δεν έχουν άλλον ακέραιο διαιρέτη εκτός από τον εαυτό τους) θα είναι άρτιος ή περιττός αριθμός;

3. Ποιο είναι το μεγαλύτερο υπόλοιπο που μπορεί να προκύψει όταν ένας διψήφιος αριθμός διαιρεθεί με το άθροισμα των ψηφίων του;

Απάντηση

1. Ο 3x θα είναι μεταξύ 50 και 80. Άρα ο x μεταξύ 16, … και 26,… άρα μεσολαβούν 10 ακέραιοι.

2. Όταν προσθέτουμε πρώτους αριθμούς και έχουμε περιτό αριθμό προσθετέων προκύπτει περιττός αριθμός ως άθροισμα. Άρα οι 99 πρώτοι αριθμοί, πλην του2, θα δώσουν περιττό αριθμό ως άθροισμα και η πρόσθεση του 2 θα δώσει επίσης περιττό αριθμό.

3. Το μεγαλύτερο άθροισμα των ψηφίων ενός διψηφίου που είναι ο 99 θα είναι 9+9=18. Ο 99 όμως ότα διαρεθεί με το 18 δίνει υπόλοιπο 9. Άρα δεν πρέπει να είναι ο ζητούμενος. Ο 98 και ο 89 δίνουν άθροισμα 17 κα οι διαιρέσεις με το 17 δίνουν υπόλοιπα 4 και 13. Με άθροισμα ψηφίων 16 είναι οι 88, 97, 79. Από αυτούς το μεγαλύτερο υπόλοιπο, 15 δίνει ο 79 . Πιο κάτω, από το 15 και μετά, αθροίσματα ψηφίων θα δίνουν υπόλοιπο μικρότερο του 15 άρα αυτός είναι ο ζητούμενος.

Μπορείτε να στείλετε τις απορίες, τις λύσεις και τις επισημάνσεις σας στον Άλκη Γαλδαδά στην διεύθυνση algaldadas@yahoo.gr.